Quanten-Wiederkehr: Alles wird wieder wie früher

Bild: Technische Universität Wien

Wenn man lange genug wartet, sehen komplizierte Systeme wieder so aus wie am Anfang. An der TU Wien konnte das nun erstmals in einem Vielteilchen-Quantensystem gezeigt werden.

In der klassischen Physik kann man sich die Poincarésche Wiederkehr durch die Bewegung von Kugeln in einer Box vorstellen. Auch wenn diese mit einem geordneten Zustand beginnt wird sich dieser Zustand irgendwann wiederholen

Bild: Technische Universität Wien

Es ist eines der bemerkenswertesten Ergebnisse der Physik: Wenn man ein kompliziertes System sich selbst überlässt, dann kehrt es irgendwann mit fast perfekter Genauigkeit zum Anfangszustand zurück. Gasteilchen beispielsweise, die zufällig und chaotisch in einem Behälter herumschwirren, werden irgendwann Positionen annehmen, die fast genau ihren Anfangspositionen entsprechen. Dieser „Poincarésche Wiederkehrsatz“ ist die Basis der modernen Chaostheorie. Seit Jahrzehnten wird untersucht, inwieweit er auch in der Welt der Quantenphysik seine Gültigkeit hat. Nun gelang es an der TU Wien erstmals, eine Form von „Poincaréscher Wiederkehr“ in Quantensystemen aus vielen Teilchen nachzuweisen. Die Ergebnisse wurden im Fachjournal „Science“ veröffentlicht.

Uralte Frage unter neuem Gesichtspunkt

Der französische Wissenschaftler Henri Poincaré beschäftigte sich am Ende des 19. Jahrhunderts mit Systemen von Teilchen, die zu kompliziert sind, um sie alle genau zu berechnen – etwa Sonnensysteme, in denen sich viele Planeten und Asteroiden gegenseitig beeinflussen, oder Gasteilchen, die ständig aneinanderstoßen. Sein überraschendes Ergebnis: Jeder physikalisch mögliche Zustand wird irgendwann auch eingenommen – zumindest in sehr guter Näherung, man muss nur ziemlich lange warten. Irgendwann werden alle Planeten zufällig eine gerade Linie bilden, irgendwann werden sich Gasteilchen zufällig zu interessanten Mustern zusammenfinden – oder genau zu dem Zustand zurückkehren, den sie zu Beginn des Experiments eingenommen haben.

Ein ähnliches Theorem lässt sich auch für Quantensysteme beweisen, allerdings gelten dort völlig andere Gesetze. „In der Quantenphysik muss man Poincarés Fragestellung völlig neu überdenken“, erklärt Prof. Jörg Schmiedmayer vom Atominstitut der TU Wien. „Der Zustand eines großen Quantensystems, das aus vielen Teilchen besteht, lässt sich prinzipiell niemals perfekt messen. Außerdem kann man die Teilchen nicht unabhängig voneinander betrachten, man muss berücksichtigen, dass sie quantenphysikalische miteinander verschränkt sind.“

Es gab bereits Versuche, den Effekt der „Poincaréschen Wiederkehr“ zu einem bestimmten Ausgangszustand mit Quantensystemen zu demonstrieren, allerdings nur mit einigen wenigen Teilchen, deren Quantenzustand man möglichst gut zu messen versuchte. Das ist extrem kompliziert, und die Zeit bis zur möglichen Wiederkehr des gewünschten Zustands steigt mit der Anzahl der Teilchen drastisch an. Das Team von Jörg Schmiedmayer wählte allerdings einen ganz anderen Zugang: „Uns interessiert nicht der vollständige innere Zustand des Systems, denn der ist ohnehin nicht ermittelbar“, sagt Bernhard Rauer, Erstautor der Publikation. „Stattdessen stellen wir die Frage: Welche beobachtbaren Größen gibt es, die uns etwas über das Gesamtsystem sagen? Und gibt es Zeiten, zu denen diese Größen wieder den Wert annehmen, den sie anfangs hatten?“

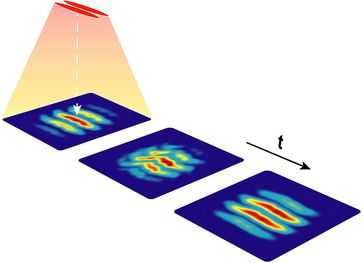
Untersucht wurde das Verhalten eines ultrakalten Gases aus tausenden Atomen, das von elektromagnetischen Feldern auf einem Chip festgehalten wurde. „Es gibt verschiedene physikalische Größen, mit denen man ein solches Quantengas charakterisieren kann – zum Beispiel Kohärenzlängen im Gas und Korrelationsfunktionen zwischen unterschiedlichen Punkten. Diese Größen geben an, wie stark die einzelnen Teilchen quantenphysikalisch in Beziehung miteinander stehen“, sagt Sebastian Erne, der für die theoretischen Berechnungen des Forschungsprojekts zuständig war. „Für unseren Alltagsverstand ist das nicht besonders intuitiv, in unserer makroskopischen Welt spielen solche Größen keine Rolle, aber in einem Quantensystem sind genau das die entscheidenden Parameter.“

Wiederkehr entdeckt – in kollektiven Größen

Beim Messen solcher Größen, die nicht einzelne Teilchenbeschreiben, sondern eine Aussage über das ganze Ensemble von Teilchen liefern, gelang es tatsächlich, die vieldiskutierten Wiederkehr-Effekte zu messen. Und nicht nur das: „Wir können mit unserem Atomchip sogar beeinflussen, wie lange die Zeitdauer sein soll, bis ein bestimmter Messzustand wiederkehrt“, berichtet Jörg Schmiedmayer. „Durch das genaue Ausmessen der Wiederkehr lernen wir viel über die kollektive Dynamik der Atome. Etwa über die Schallgeschwindigkeit im Gas oder wie Dichtewellen aneinander streuen.“

Die alte Frage, ob auch Quantensysteme zum Ursprungszustand zurückkehren, lässt sich also mit ja beantworten – allerdings ein bisschen anders als man bisher dachte. Anstatt dem vollständigen inneren Zustand eines Systems hinterherzulaufen, der ohnehin nie genau gemessen werden kann, ist es sinnvoller, sich auf die Größen zu konzentrieren, die quantenmechanisch tatsächlich beobachtbar sind. Und diesen Größen kann man dabei zusehen, wie sie von ihrem Anfangszustand wegdriften – und schließlich wieder zurückkehren.

Quelle: Technische Universität Wien